The point of this lab is to search and backtrack. The domain will
be a maze, and it will be a relatively simple maze. The system
should try a path. If it fails it should backtrack and try a
different path.
- Here is a maze:
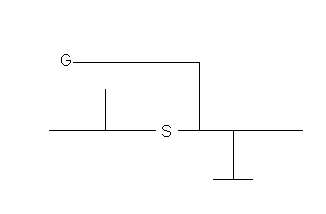
- S is the start, and G is the goal.
Encode the maze as a series of facts. I did it with
13 facts.
- Simplifications:
- At any point there will be at most three choices,
with one of those choices being where you came from; this means
that you only need to remember one possible place to back up to
at each point.
- There will be no cycles. This means that you can't get back
to a place you've already been without backing up.
- Make a system that solves every maze with the two simplifications.
There are at least three ways to do this:
- Solve this particular problem, then try to fix it up.
- Solve it in sections. Here's the way I broke the problem down.
- Make a rule that moves the user. Be careful, if you run, the
rule might loop (use the Execution menu with the Halt item).
- Modify the rule so that it remembers where it's been and
doesn't go back.
- Implement backtracking. I did this in three steps.
- Make a new rule that works when there are two options, travel
down one and stack the other. I had to use a neq test on
this. I also used (declare (salience 10)) so that the
two option rule is preferred over the one option rule.
- Modify the rule so that it stacks the alternative. I used
a stackHt and stack variable and filled in the untaken path.
I only kept one instance of stackHt but had one variable
for each stack element.
- Add a rule to backtrack when there are no other options. That
is, if there is a deadend, pop the stack and move to that
location.
- Add a rule to stop when the user is at the goal.
- Try to solve it all in one step. The eventual solution I get
has seven rules.
- Design your own maze and show the system running on it.
- Are you confident it will run on all reasonable mazes?
- What will happen if there are cycles?
- What would you do if there were more than three choices at any
one point?